Adaptive finite-time fan-coil outlet wind temperature control for the ASHPAC system

Chen, Xiaofei; Li, Chao; Yang, Qinmin

doi:10.3389/fenrg.2022.954351

ORIGINAL RESEARCH article

Front. Energy Res., 18 November 2022
Sec. Process and Energy Systems Engineering
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.954351

Adaptive finite-time fan-coil outlet wind temperature control for the ASHPAC system

Xiaofei Chen¹,

Chao Li¹ and

Qinmin Yang^1,2*

¹College of Control Science and Engineering, Zhejiang University, Hangzhou, Zhejiang, China
²Huzhou Institute of Zhejiang University, Huzhou, China

In this paper, an adaptive finite-time fan-coil outlet wind temperature control scheme is proposed for the air-source heat pump air-conditioning system. First, a correction module is introduced to compensate the first-order damp elements in the temperature sensor to capture the temperature in real-time. Then, a simple neural network is employed to approximate the unknown and nonlinear functions of the system. On this basis, an adaptive finite-time neural controller is developed, and the finite-time convergence of temperature regulation error is ensured. The stability of the studied fan-coil control is guaranteed by rigorous Lyapunov proof. Finally, two simulation examples are carried out to verify the effectiveness of the proposed control scheme.

1 Introduction

Peaking carbon dioxide emissions and carbon neutrality play an important role on the national strategic level (Jia and Lin, 2021) to realize the “30 ⋅ 60” goal and the “14th Five-Year Plan” for power development. It is urgent to expand the scale of renewable energy utilization and improve the energy efficiency. The ASHPAC system utilizes the solar radiating energy contained in the air as the cooling or heating source (Yu et al., 2021; Yong et al., 2021). It follows the reversible Carnot cycle when working and drives the compressor through a small amount of electricity to realize energy transfer. Compared with the general HVAC system (Magraner et al., 2010), its COP is higher. As the core component of the indoor loop of the ASHPAC system, the fan-coil performance determines the comfort of the indoor environment (Kayaci, 2020). To create a constant and comfortable indoor environment, it is of great significance to design a flexible, reliable, and stable algorithm to improve the control accuracy and response rate of the fan-coil outlet temperature.

Recently, numerous research results on the temperature control of the ASHPAC system have been reported. In Yang et al. (2007) and Grassi and Tsakalis (2000), a conventional PID scheme was proposed to deal with the temperature control problem of the ASHPAC system, but the accuracy and effectiveness would be degraded in a realistic ambience because of the varying load conditions. Thus, some modified PID schemes were proposed to improve the control performance [see (Li et al., 2013; Xu et al., 2019; Wrat et al., 2020; Li et al., 2013; Xu et al., 2019; Wrat et al., 2020) and the references therein], where the PID parameters could be adjusted online by fuzzy reasoning, according to varying working conditions. However, these schemes are dependent on preset fuzzy rules, which require a large amount of professor knowledge, while it is difficult to establish a universal fuzzy rule base for different systems. In Han et al. (2021), a PSO fuzzy PID scheme was proposed to reduce inevitable randomness, which requires a large amount of computing resources. In Wang et al. (2021), a nonlinear MPC algorithm was proposed to regulate the temperature of outlet water of the transcritical CO₂ ASHP water heater. This scheme ensures true real-time dynamic optimization, but it requires accurate models, which are difficult to obtain. In Lissa et al. (2021), a DRL algorithm was applied to hot water tank temperature control, but it needs huge computational resources. Thus, it is still a challenging work to design an adaptive controller without prior knowledge on the requirement and accurate model for the ASHPAC system.

On the other hand, the aforementioned literature only guarantees the asymptotical convergence of the temperature regulation error, which means that the convergence time of the temperature regulation error is infinite. Different from the asymptotically stable control, the finite-time control can realize that the state tends to the equilibrium point within a finite time. With the satisfactory characteristics, such as faster convergence performance, higher control precision, and better robustness against disturbances and uncertainties, the finite-time control has been widely applied to various nonlinear systems (Yu et al., 2005; Chen et al., 2018; Li et al., 2019; Xie and Chen, 2022; Yu et al., 2005; Chen et al., 2018; Li et al., 2019; Xie and Chen, 2022). In Yu et al. (2005), a continuous finite-time control scheme was proposed for rigid robotic manipulators by constructing a new form of terminal sliding modes. Li et al. (2019) investigated the problem of adaptive finite-time tracking control for strict-feedback nonlinear continuous-time systems. In Chen et al. (2018) and Xie and Chen (2022), two different control strategies were put forward to deal with the finite-time attitude stabilization problem of the rigid spacecraft. In Emami-Naeini et al. (1994), an approximate finite-time control scheme was applied to temperature profile tracking in rapid thermal processing systems. In Chen et al. (2019), a finite-time controller was designed for the double-layer Peltier system based on a finite-time observer, such that the temperature error can be converged within a finite time. To this end, it is meaningful to design a finite-time outlet wind temperature controller for improving both the transient performance and steady performance of the ASHPAC system. However, the relevant research works on finite-time outlet wind temperature control of the ASHPAC system have not been reported.

Motivated by the aforementioned observations, an adaptive finite-time neural fan-coil outlet wind temperature control scheme is proposed for the ASHPAC system. The main contributions are summarized as follows.

Compared with the asymptotically stable control (Grassi and Tsakalis, 2000; Yang et al., 2007; Li et al., 2013; Xu et al., 2019; Wrat et al., 2020; Han et al., 2021; Lissa et al., 2021; Wang et al., 2021; Grassi and Tsakalis, 2000; Yang et al., 2007; Li et al., 2013; Xu et al., 2019; Wrat et al., 2020; Han et al., 2021; Lissa et al., 2021; Wang et al., 2021), a finite-time neural controller is systematically presented such that the temperature regulation error is ensured to converge into a small region around the origin within a finite time.

A correction module is introduced to compensate the first-order damp elements in the temperature sensor to capture the temperature in real time. Moreover, a neural network-based adaptive law is designed to compensate for the unknown and nonlinear functions of the ASHPAC system such that the model knowledge of the system is not required in prior.

The rest of this article is outlined as follows: in Section 2, the mathematical model is presented. The correction module of a thermistor is given in Section 3, and the adaptive finite-time control design and stability analysis are given in Section 4. In Section 5, the obtained results are supported by numerical simulations. Finally, the conclusion is summarized in Section 6.

2 System description

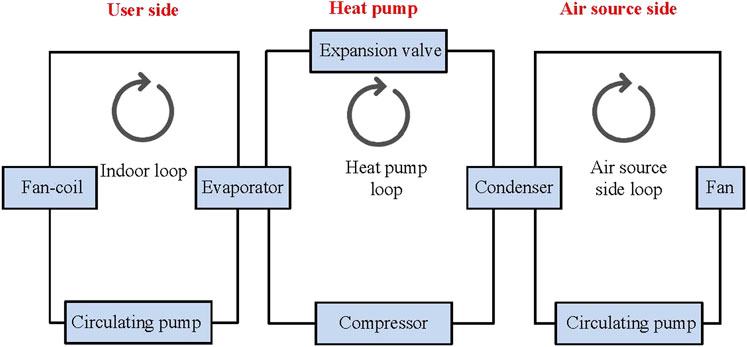
The ASHPAC system contains the air-source side loop, the heat pump loop, and the indoor loop (Xiao, 2010), which is shown in Figure 1.

FIGURE 1

FIGURE 1. Diagram of the ASHPAC system.

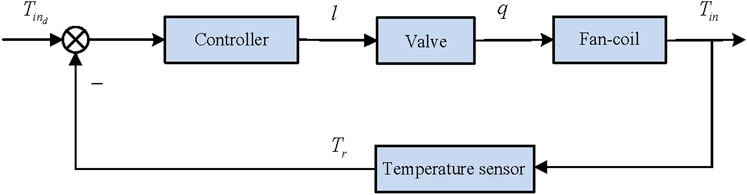
As shown in Figure 2, the control structure of the fan-coil consists of the flow-regulating valve, the fan-coil, and the temperature sensor (Zhang et al., 2021). It is found from Figure 2 that l and q are the spool stroke and chilled water flow at a certain opening, respectively. T_in is the output wind temperature of the fan-coil, T_r is the output value of the temperature sensor, and $T_{i n_{d}}$ is the tracking target.

FIGURE 2

FIGURE 2. Control structure of the fan-coil.

Flow-regulating valves generally have four ideal flow characteristics, such as the linear characteristic, parabolic characteristic, quick opening characteristic, and equal percentage characteristic (Dutta et al., 2014).

The equal percentage flow capacity increases exponentially with the spool stroke. Equal increases in valve travel produce equal percentage changes in the existing flow coefficients. The equal percentage flow characteristic is given by Mala and Li (1999):

\frac{d (\frac{q}{q_{\max}})}{d (\frac{l}{L})} = K_{v} \frac{q}{q_{\max}} . (1)

Using the boundary conditions

\{\begin{cases} q = q_{\min}, l = 0 \\ q = q_{\max}, l = L, \end{cases} (2)

one can obtain

\frac{q}{q_{\max}} = {(\frac{q_{\max}}{q_{\min}})}^{(\frac{l}{L} - 1)} . (3)

If $R = \frac{q_{\max}}{q_{\min}}$ is defined as the regulating ratio, then Eq. 3 can be rewritten as

q = q_{\min} R^{\frac{l}{L}}, (4)

where L is the maximum spool stroke of the valve, K_v is the magnification factor, q_max is the maximum flow rate, and q_min is the minimum flow rate.

The fan-coil is the terminal device of the heat pump air-conditioning system, which is a surface heat exchanger used to reduce or increase the room temperature and create an indoor air environment suitable for human comfort.

Based on the law of energy conservation, by ignoring the heat storage effect of the fan-coil, the mathematical model can be simplified into a single-capacity first-order differential equation (Wu, 2015):

\begin{aligned} K_{a} \frac{d T_{i n}}{d t} + T_{i n} = - K_{b} q + K_{c}, \end{aligned} (5)

where $K_{a} = \frac{C_{V} V_{f c} ρ}{G_{a c} c_{1}}$ , $K_{b} = \frac{Δ T_{d} c_{2}}{G_{a c} c_{1}}$ , and $K_{c} = T_{0} + \frac{P_{0}}{G_{a c} c_{1}}$ ; C_V is the constant volume-specific heat of air, V_fc is the volume of air circulated into the fan-coil, ρ is the density of air, G_ac is the air flow rate of the fan-coil, c₁ is the specific heat of air, ΔT_d is the chilled water temperature difference, c₂ is the specific heat of chilled water, T₀ is the inlet air temperature of the fan-coil, and P₀ is the total power of the fan-coil. Among these parameters, C_V, ρ, c₁, and T₀ are determined by the actual temperature, which are uncertain.

A thermistor is often used as the temperature sensor in the closed-loop control system of air-conditioning, and the relationship between its sensed temperature T_in and output temperature T_r is given by

T \frac{d T_{r}}{d t} + T_{r} = T_{i n}, (6)

where T is the time constant of the thermistor.

3 Correction module of the thermistor

The existence of the time constant makes the change of the thermistor thermal potential always lag behind the perceived temperature variation. Based on (6), the characteristic of the temperature sensor can be regarded as a first-order inertial element, which can be described by G_ts(s), that is,

G_{t s} (s) = \frac{1}{T s + 1} . (7)

The temperature control of the fan-coil is required to be fast and accurate; thus, the influence of T cannot be ignored. To improve the measurement accuracy of the thermistor temperature sensor, we broaden the bandwidth of the feedback element by connecting a correction element in series (Li et al., 2005), that is,

\begin{aligned} W (s) & = G_{t s} (s) \cdot H (s) \\ = \frac{1}{T s + 1} \cdot \frac{T s + 1}{T^{'} s + 1}, \end{aligned} (8)

where T′ < T, $H (s)$ , and $W (s)$ are the transfer functions of the correction element and the feedback loop after correcting.

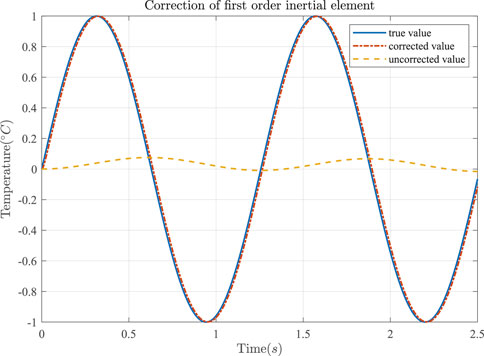
As shown in Figure 3, when the thermistor with a large time constant is used to detect the temperature directly, its output distortion is large. After adding the correction element, as long as T′ is reasonably selected, the error between the sensed temperature and the output temperature can be eliminated.

FIGURE 3

FIGURE 3. Correction of the first-order inertial element.

4 Adaptive finite-time control

4.1 Controller design

The introduction of the correction module eliminates the lag of the thermistor, so the characteristic of the temperature sensor can be regarded as unity feedback. Based on the characteristic of the flow-regulating valve in (4), for ease of presentation, one should observe

q = q_{\min} u, (9)

where $u = R^{\frac{l}{L}}$ .

According to (5) and (9), one can obtain

{\dot{T}}_{i n} = \frac{1}{K_{a}} (- T_{i n} - K_{b} q_{\min} u + K_{c}), (10)

where K_a, K_b, and K_c are uncertain in the controller design; let $θ_{1} = - \frac{1}{K_{a}}$ , $θ_{2} = - \frac{K_{b} q_{\min}}{K_{a}}$ , and $d = \frac{K_{c}}{K_{a}}$ , then the fan-coil control system becomes

{\dot{T}}_{i n} = θ_{1} T_{i n} + θ_{2} u + d . (11)

The tracking error e is defined as

e = T_{i n} - T_{i n_{d}} . (12)

Differentiating (12) yields

\begin{align} \dot{e} & = {\dot{T}}_{i n} - {\dot{T}}_{i n_{d}} \\ = θ_{1} T_{i n} + θ_{2} u + d \\ = θ_{2} (\frac{θ_{1}}{θ_{2}} T_{i n} + u + \frac{d}{θ_{2}}) \\ = θ_{2} (g + u), \end{align} (13)

where $g = \frac{θ_{1}}{θ_{2}} T_{i n} + \frac{d}{θ_{2}}$ is the lumped uncertainty.

The lumped uncertainty g in (13) can be approximated by the neural network (NN), given by

g = W^{T} Φ (T_{i n}) + ε, (14)

where ɛ is the approximation error bounded by |ɛ| ≤ ɛ_N, with ɛ_N being a small positive constant, and Φ(T_in) is the NN basis function with the following sigmoid form:

Φ (T_{i n}) = \frac{l_{1}}{l_{2} + \exp (- T_{i n} / l_{3})} + l_{4} . (15)

With the NN approximation, the finite-time controller is designed as

u = - k_{1} e - k_{2} {s i g}^{α} (e) - {\hat{W}}^{T} Φ, (16)

where k₁ > 1/2, k₂ > 0, 0 < α < 1, sig^α(e) = |e|^α sgn(e), and sgn (⋅) denote the sign function, and $\hat{W}$ is the estimation of W.

The adaptive update law of $\hat{W}$ is given by

\dot{\hat{W}} = e Φ - σ \hat{W}, (17)

where σ is a positive constant.

4.2 Stability analysis

To analyze the finite-time stability of the fan-coil control system, several useful lemmas are provided as follows.

5 Simulation results

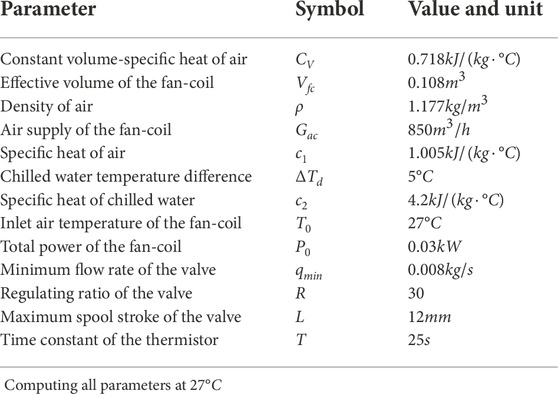
We choose the fan-coil “SF05RC” produced by PHNIX and the electric small flow-regulating valve produced by VTON as objects and compute the parameters of the system in Table 1, and the units of measurements of these terms are provided.

TABLE 1

TABLE 1. Parameters of the system.

The models of the flow-regulating valve, the fan-coil, and the temperature sensor are given as

q = 0.008 \cdot 3 0^{\frac{l}{12}}, (31)

0.3275 \frac{d T_{i n}}{d t} + T_{i n} = - 75.19 q + 27.107 . (32)

Based on this system model, the proposed adaptive finite-time controller is then utilized. Also, the unknown parameters are initialized with K_a = 0.3275s, $K_{b} = 75.1900 (° C \cdot s) / k g$ , and K_c = 27.1070°C. The parameters of the finite-time controller (16) and adaptive update law (17) are chosen as $k_{1} = 2, k_{2} = 2, α = \frac{5}{7}$ and σ = 0.1. The parameters of the sigmoid function (15) are set as l₁ = 12, l₂ = 10, l₃ = 6, and l₄ = 2.

5.1 Simulation with the step signal

The tracking objective is chosen as Table 2 for controlling the step signal, where r(t) is the step signal.

TABLE 2

TABLE 2. Objective of the tracking step signal.

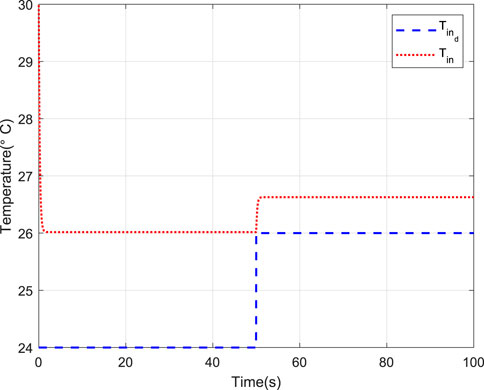
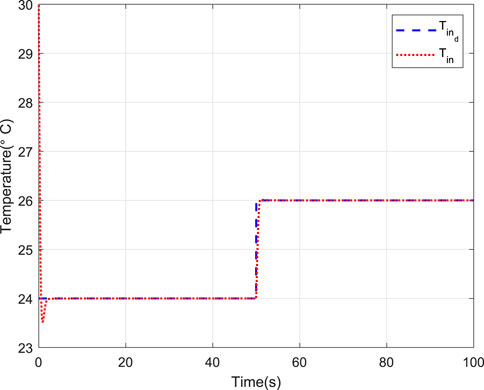
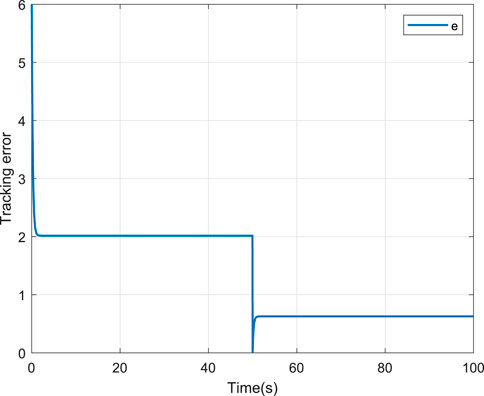
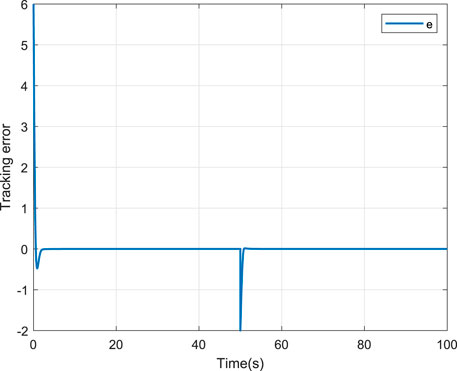
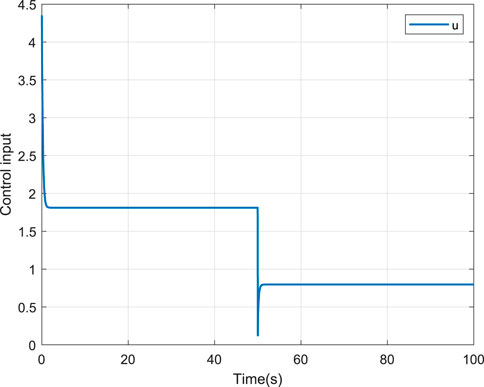
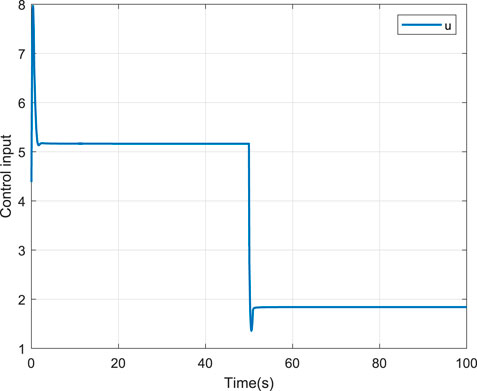
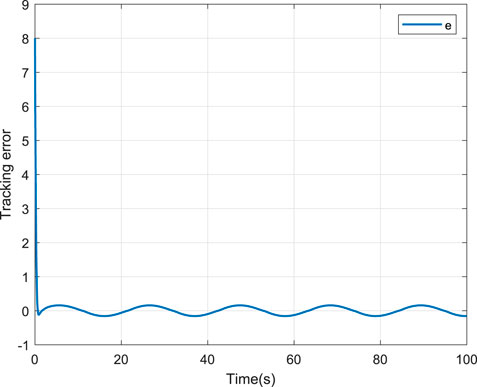
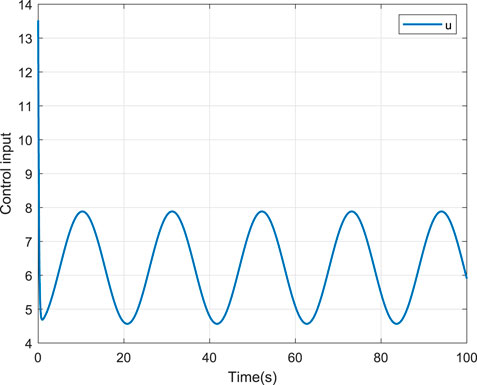
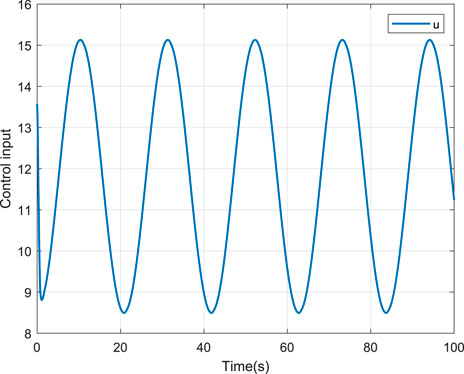
To verify the effectiveness of the proposed scheme, two comparative cases, that is, without and with the NN compensation are provided. For fair comparison, the parameters of the two schemes are selected the same. The corresponding simulation results are depicted in Figures 4–9. Figure 4 shows the tracking performance without NN compensation. From Figure 4, it can be seen that the output wind temperature of the fan-coil cannot reach the first target (24°C) and the second target (26°C) in a short time. Figure 5 depicts the tracking performance with NN compensation. It can be found from Figure 5 that the tracking performance is superior. Compared with Figures 4, 5, we can conclude that the finite-time controller can realize fast and accurate temperature regulation with the help of the NN compensation. The temperature tracking error e without and with NN compensation are shown in Figures 6, 7, respectively. From Figure 6, it can be seen that the temperature tracking error e is large. From Figure 7, we can see that when the temperature changes rapidly, the temperature tracking error e becomes lager, but the temperature tracking error e is small overall. In addition, the control input u without and with NN compensation are depicted in Figures 8, 9, respectively. From Figures 8, 9, it can be obtained that the larger control input is required with NN compensation.

FIGURE 4

FIGURE 4. Tracking performance without NN compensation.

FIGURE 5

FIGURE 5. Tracking performance with NN compensation.

FIGURE 6

FIGURE 6. Tracking error without NN compensation.

FIGURE 7

FIGURE 7. Tracking error with NN compensation.

FIGURE 8

FIGURE 8. Control input without NN compensation.

FIGURE 9

FIGURE 9. Control input with NN compensation.

5.2 Simulation with the cosine signal

Furthermore, we also simulate the proposed adaptive control algorithm with the cosine signal, and the objectives are chosen as Table 3.

TABLE 3

TABLE 3. Objectives of the tracking squarewave and ramp signals.

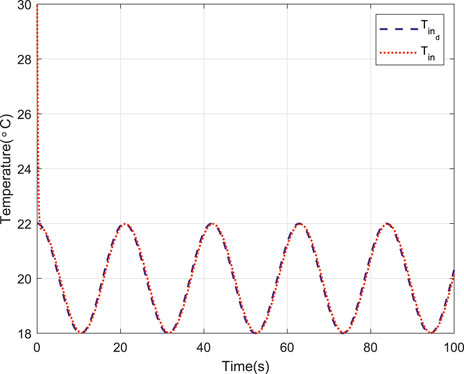
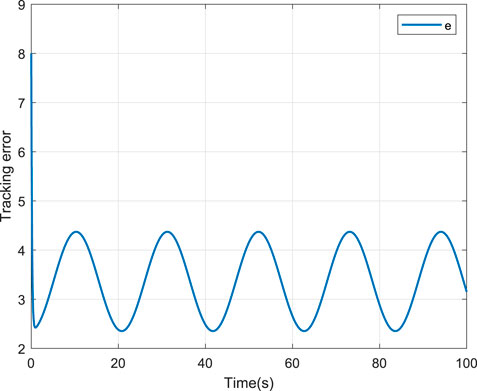
The results of the tracking cosine signal are shown in Figures 10–15. Figure 10 shows the tracking performance without NN compensation. From Figure 10, it can be seen that the output wind temperature of the fan-coil cannot reach the target temperature. Figure 11 depicts the tracking performance with NN compensation. It can be found from Figure 11 that the tracking performance is superior with a fast response. The temperature tracking error e without and with NN compensation are shown in Figures 12, 13, respectively. From Figures 12, 13, we can again obtain that the temperature tracking error e is smaller with the aid of NN compensation. Moreover, the control input u without and with NN compensation are depicted in Figures 14, 15, respectively. From Figures 14, 15, we can again obtain that the larger control input is required with NN compensation.

FIGURE 10

FIGURE 10. Tracking performance without NN compensation.

FIGURE 11

FIGURE 11. Tracking performance with NN compensation.

FIGURE 12

FIGURE 12. Tracking error without NN compensation.

FIGURE 13

FIGURE 13. Tracking error with NN compensation.

FIGURE 14

FIGURE 14. Control input without NN compensation.

FIGURE 15

FIGURE 15. Control input with NN compensation.

From Figures 4–15, it can be concluded that the proposed control scheme can achieve the satisfactory tracking performance (e.g., fast convergence speed and accurate tracking error) with the help of NN compensation.

6 Conclusion

In this paper, an adaptive finite-time fan-coil outlet wind temperature control scheme has been developed for the air-source heat pump air-conditioning system. A correction module is introduced to compensate for the first-order damp elements in the temperature sensor to capture the temperature in real time. On this basis, an adaptive finite-time neural controller is developed. Different from the asymptotically stable control, the proposed finite-time temperature control can ensure that the temperature regulation error be converged into a small region around the origin within a finite time, which further improves the tracking performance of the ASHPAC system. Finally, two simulation examples have been carried out to demonstrate the effectiveness of the proposed scheme.

Data availability statement

The datasets generated and analysed during the current study are not publicly available as the data also forms part of an ongoing study, but are available from the corresponding author on reasonable request.

Author contributions

CL and QY contributed to the conceptionand design of the study. XC organized the database and performed the statistical analysis. All authors contributed in drafting the manuscript and revision. They approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, C., Ding, S., and Li, S. (2019). Finite-time control for double-layer Peltier system based on finite-time observer. Adv. Mech. Eng. 11 (3), 168781401983685–10. doi:10.1177/1687814019836852

CrossRef Full Text | Google Scholar

Chen, Q., Xie, S., Sun, M., and He, X. (2018). Adaptive nonsingular fixed-time attitude stabilization of uncertain spacecraft. IEEE Trans. Aerosp. Electron. Syst. 54 (6), 2937–2950. doi:10.1109/taes.2018.2832998

CrossRef Full Text | Google Scholar

Dutta, S., Sarkar, A., Samanta, K., Das, R., and Ghosh, A. (2014). “Supervision of control valve characteristics using PLC and creation of HMI by SCADA,” in 2014 First International Conference on Automation, Control, Energy and Systems (ACES), 1–5.

CrossRef Full Text | Google Scholar

Emami-Naeini, A., Kabuli, M., and Kosut, R. (1994). “Finite-time tracking with actuator saturation: Application to RTP temperature trajectory following,” in 33rd IEEE Conference on Decision and Control, 73–78.

Google Scholar

Grassi, E., and Tsakalis, K. (2000). PID controller tuning by frequency loop-shaping: Application to diffusion furnace temperature control. IEEE Trans. Control Syst. Technol. 8 (5), 842–847. doi:10.1109/87.865857

CrossRef Full Text | Google Scholar

Han, Q., Yang, Y., Yu, J., Gu, H., Ren, X., and Gao, L. (2021). “Design of heat pump temperature control system based on particle swarm optimization fuzzy PID,” in 2021 36th Youth Academic Annual Conference of Chinese Association of Automation (YAC), 442–446.

Google Scholar

Jia, Z., and Lin, B. (2021). How to achieve the first step of the carbon-neutrality 2060 target in China: The coal substitution perspective. Energy 233, 121179. doi:10.1016/j.energy.2021.121179

CrossRef Full Text | Google Scholar

Kayaci, N. (2020). Energy and exergy analysis and thermo-economic optimization of the ground source heat pump integrated with radiant wall panel and fan-coil unit with floor heating or radiator. Renew. Energy 160, 333–349. doi:10.1016/j.renene.2020.06.150

CrossRef Full Text | Google Scholar

Li, H., Zhao, S., He, W., and Lu, R. (2019). Adaptive finite-time tracking control of full state constrained nonlinear systems with dead-zone. Automatica 100, 99–107. doi:10.1016/j.automatica.2018.10.030

CrossRef Full Text | Google Scholar

Li, Q., Li, G., and Zhang, T. (2005). The thermo-couple dynamic characteristic correction. Electron. Meas. Technol. 3 (18), 32–33.

Google Scholar

Li, Y., Cai, C., Lee, K., and Teng, F. (2013). A novel cascade temperature control system for a high-speed heat-airflow wind tunnel. Ieee. ASME. Trans. Mechatron. 18 (4), 1310–1319. doi:10.1109/tmech.2013.2262077

CrossRef Full Text | Google Scholar

Lissa, P., Deane, C., Schukat, M., Seri, F., Keane, M., and Barrett, E. (2021). Deep reinforcement learning for home energy management system control. Energy AI 3, 100043. doi:10.1016/j.egyai.2020.100043

CrossRef Full Text | Google Scholar

Magraner, T., Montero, A., Quilis, S., and Urchueguía, J. F. (2010). Comparison between design and actual energy performance of a HVAC-ground coupled heat pump system in cooling and heating operation. Energy Build. 42 (9), 1394–1401. doi:10.1016/j.enbuild.2010.03.008

CrossRef Full Text | Google Scholar

Mala, G., and Li, D. (1999). Flow characteristics of water in microtubes. Int. J. heat fluid flow 20 (2), 142–148. doi:10.1016/s0142-727x(98)10043-7

CrossRef Full Text | Google Scholar

Wang, W., Zhao, Z., Zhou, Q., Qiao, Y., and Cao, F. (2021). Model predictive control for the operation of a transcritical CO2 air source heat pump water heater. Appl. Energy 300, 117339. doi:10.1016/j.apenergy.2021.117339

CrossRef Full Text | Google Scholar

Wrat, G., Bhola, M., Ranjan, P., Mishra, S. K., and Das, J. (2020). Energy saving and Fuzzy-PID position control of electro-hydraulic system by leakage compensation through proportional flow control valve. ISA Trans. 101, 269–280. doi:10.1016/j.isatra.2020.01.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, D. (2015). Modeling and simulation of central air-conditioning automatic control system. Hohhot, China: Inner Mongolia University.

Google Scholar

Xiao, X. (2010). Study of energy-saving control system in ground-source heat pump central air-conditioner. Changsha, China: Hunan Normal University.

Google Scholar

Xie, S., and Chen, Q. (2022). Adaptive nonsingular predefined-time control for attitude stabilization of rigid spacecrafts. IEEE Trans. Circuits Syst. Ii. 69 (1), 189–193. doi:10.1109/tcsii.2021.3078708

CrossRef Full Text | Google Scholar

Xie, S., Chen, Q., and He, X. (2022). Predefined-time approximation-free attitude constraint control of rigid spacecraft. IEEE Trans. Aerosp. Electron. Syst., 1–11. doi:10.1109/TAES.2022.3183550

CrossRef Full Text | Google Scholar

Xu, Y., Jia, M., and Chen, S. (2019). “Research on electric vehicle heat pump air conditioning control system based on fuzzy PID algorithm,” in 2019 Chinese Automation Congress (CAC), 1155–1159.

CrossRef Full Text | Google Scholar

Yang, Z., Pedersen, G. K. M., Larsen, L. F. S., and Thybo, H. (2007). “Modeling and control of indoor climate using a heat pump based floor heating system,” in IECON 2007 - 33rd Annual Conference of the IEEE Industrial Electronics Society, 2985–2990.

CrossRef Full Text | Google Scholar

Yong, H. E., Chung, Y., Min, S. P., Hong, S. B., and Min, S. K. (2021). Deep learning-based prediction method on performance change of air source heat pump system under frosting conditions. Energy 228, 120542. doi:10.1016/j.energy.2021.120542

CrossRef Full Text | Google Scholar

Yu, M., Li, S., Zhang, X., and Zhao, Y. (2021). Techno-economic analysis of air source heat pump combined with latent thermal energy storage applied for space heating in China. Appl. Therm. Eng. 185, 116434. doi:10.1016/j.applthermaleng.2020.116434

CrossRef Full Text | Google Scholar

Yu, S., Yu, X., Shirinzadeh, B., and Man, Z. (2005). Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 41 (11), 1957–1964. doi:10.1016/j.automatica.2005.07.001

CrossRef Full Text | Google Scholar

Zhang, T., Li, Y., Yang, Q., Meng, W., and Jiang, H. (2021). Adaptive fan-coil outlet wind temperature control with correction module of thermistor for the ASHPAC system. in 2021 China Automation Congress (CAC), 7955–7960.

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviations

ASHPAC air-source heat pump air-conditioning

HVAC heating ventilation air-conditioning

COP coefficient of performance

PSO particle swarm optimization

MPC model predictive control

ASHP air-source heat pump

DRL deep reinforcement learning

PID proportional integral derivative.

Keywords: renewable energy, ASHPAC, control, finite-time control (FTC), adaptive control

Citation: Chen X, Li C and Yang Q (2022) Adaptive finite-time fan-coil outlet wind temperature control for the ASHPAC system. Front. Energy Res. 10:954351. doi: 10.3389/fenrg.2022.954351

Received: 27 May 2022; Accepted: 24 October 2022;
Published: 18 November 2022.

Edited by:

Yanping Du, Shanghai Jiao Tong University, China

Reviewed by:

Elisa Marrasso, University of Sannio, Italy
Zhu Jiang, Southeast University, Nanjing, China

Copyright © 2022 Chen, Li and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Qinmin Yang, qmyang@zju.edu.cn

ORIGINAL RESEARCH article

Adaptive finite-time fan-coil outlet wind temperature control for the ASHPAC system

1 Introduction

2 System description

3 Correction module of the thermistor

4 Adaptive finite-time control

4.1 Controller design

4.2 Stability analysis

5 Simulation results

5.1 Simulation with the step signal

5.2 Simulation with the cosine signal

6 Conclusion

Data availability statement

Author contributions

Conflict of interest

Publisher’s note

References

Nomenclature

Abbreviations

This article is part of the Research Topic

People also looked at